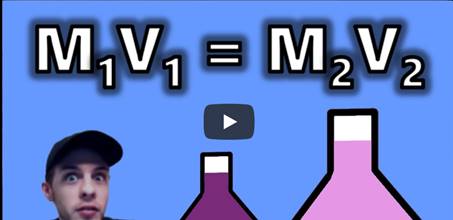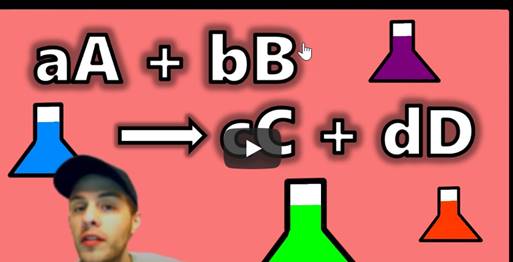Unit 26:
Solution Chemistry

Unit Overview:
In
the last few units, you defined solutions, explored solubility, described
solutions, and calculated solution concentration.
In
this unit, you will apply your knowledge of solution concentration to explore
solution stoichiometry problem-solving.
How do you make a solution of known
concentration?
In
order to make a solution of a specific concentration, follow these steps:
1. Calculate the mass of solute required. You will need to complete a molarity problem to calculate this. First, use the given molarity as a conversion
factor to convert the volume of solution to moles of solute. Then, use the molar mass of the as a
conversion factor to convert the moles to the mass of solute. [So, you may want
to have your Interactive Periodic Table pulled up so that you can access it for
molar mass values.]
2.
Carefully, mass out the calculated
amount of solute. In the lab, you use a balance to
carefully measure the required amount of solute.
3.
Carefully measure the volume
of water required to make the solution. In
the lab, use a graduated cylinder (or a volumetric flask) to measure the exact
volume of water to make the solution.
4.
Dissolve the solute in the
solvent. Dissolve the solute in the solvent to make
the exact volume of the exact molarity.
Example 1: Describe how you would make 250.0 mL of a
1.25 M NaCl solution.
|
Step 1: Calculate the mass of solute required. |
|||
|
Start with the volume of a solution: |
First, use molarity as a conversion
factor to convert to moles: |
Then, use molar
mass as a conversion factor to convert to mass: |
To
find the mass of solute required! |
|
250.0 mL |
1.25 mol NaCl 1000 mL |
58.44 g NaCl mol NaCl |
= 18.3 g NaCl |
|
Step 2: Carefully mass out the calculated amount of
solute. Use a balance to carefully measure
18.3 g of NaCl. |
|
||
|
Use a graduated cylinder to measure
250 mL volume of water into a beaker.
|
Step 3: Carefully measure the volume of water
required to make the solution. |
Or, use a volumetric flask to
measure exactly 250 mL of water. |
|
|
|
Step 4: Dissolve the solute in the solvent. Use a stirring rod to dissolve the
salt in the water. |
||
Watch the following video to help further you
visualize and understand how to make a solution of known concentration:
Practice 1: Determine the mass
of solute that would be required to make each of the following solutions.
1. 40 mL of 0.7 M KBr
2. 300 mL of 2.5 M HCl
3. 70 mL of 0.5 M BaS
How do you dilute a solution?
Solutions
are generally described as concentrated or dilute. A concentrated solution describes a solution that has a relatively
larger amount of solute dissolved in the solvent. A dilute
solution describes a solution that has a relatively smaller amount of
solute dissolved in the solvent.
In a
microscopic representation of the two general categories of solutions, a
concentrated solution has a greater number of solute particles between the
water molecules. A dilute solution has a
smaller number of solute particles between the water molecules.
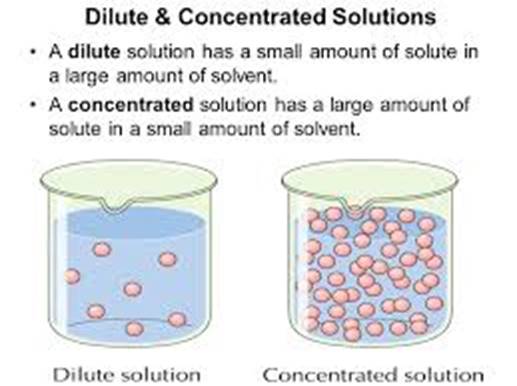
A concentrated
solution can be diluted by adding water to it.
To determine how to dilute a solution, the dilution equation is
utilized.
The
dilution equation: VcMc = VdMd
Where:
Vc =
volume of the concentrated solution
Mc =
molarity of the concentrated solution
Vd =
volume of the dilute solution
Md =
molarity of the dilute solution
To
solve dilution problems, carefully solve the “missing variable.”
Example 2: If the solution prepared in
the above example 1 is diluted to 750 mL, what is the concentration of the
dilute solution?
To
solve this problem, use the dilution equation:
VcMc
= VdMd
The
question asks me to calculate the molarity of the dilute solution, so that is
the “missing variable,”
VcMc
= VdMd
The
other 3 variables are known. The
solution from example 1 is the concentrated solution, so those values are
placed into the equation.
(250
mL)(1.25 M) = VdMd
We
are told that the solution is diluted to 750 mL, so that is the volume of the
dilute solution.
(250
mL)(1.25 M) = (750 mL)Md
Then,
solve for the missing variable:
0.42
M = Md
Watch the following video to help further you
understand how to dilute a solution to a specific concentration:
Practice
2: Complete the practice problems in this online quiz.
How are reactions of solutions
mathematically analyzed?
In
unit 22, you explored stoichiometry as a method to analyze the relative amounts
of reactants and products involved in a chemical reaction. In this unit, you will expand your
stoichiometry skills to include the use of concentration within this analysis.
When
reactions include solutions, molarity is used in the stoichiometry
problem-solving process to relate the volume of solution to the moles of
reactant. Molarity is an additional conversion factor that is used with molar
mass and coefficients.
Example 3: If the diluted solution
from the above example 2 reacts with an excess of silver nitrate, how many
grams of silver chloride will precipitate?
NaCl
(aq) +
AgNO3 (aq)
→ AgCl (s) +
NaNO3 (aq)
|
Start
with the given substance: |
Convert
the volume to moles, using the molarity as a conversion factor: |
Relate
moles of reactant to moles of product with coefficients: |
Convert
the moles to mass, using molar mass: |
To calculate the mass of
precipitate! |
|
750 mL |
0.42 mol NaCl 1000 mL
|
1 mol AgCl 1 mol NaCl |
143.32 g AgCl 1 mol AgCl |
= 45.1 g AgCl |
Watch the following video to help you connect your
understandings of solutions to your understandings of stoichiometry:
Practice 3: Complete the practice
problems.
Solve
each of the following solution stoichiometry problems:
1.) If
25.0 mL of 0.350 M NaOH is added to a copper (II) sulfate solution, how many
grams of copper (II) hydroxide will precipitate?
2
NaOH (aq) + CuSO4 (aq)
→ Cu(OH)2 (s) + Na2SO4
(aq)
2.) How
many mL of 0.715 M HCl is required to completely react with 1.25 grams of
sodium carbonate?
2
HCl (aq) + Na2CO3 (s)
→ 2 NaCl (aq) + H2O
(l) +
CO2 (g)
3.) How
many mL of 0.280 M barium nitrate are required to completely react with 25.0 mL
of 0.350 M aluminum sulfate?
3
Ba(NO3)2 (aq) + Al2(SO4)3 (aq) →
3 BaSO4(s) + 2 Al(NO3)3 (aq)
ChemLab:
Concentration Phet Simulation
Overview:
When
describing a solution, its concentration indicates the relative amounts of
solute and solvent. Concentration
increases as the amount of solute in a fixed amount of solvent increases. In this lab, you will explore concentration
by examining the relative amounts of solute and solvent.
Embed
the Phet Simulation: Concentration
Directions:
1. Download the Student
Exploration Sheet.
2. Practice using the Phet simulation.
3. Follow the instructions in the Exploration
Sheet to explore the relationships between the amount of solute and
solvent. Be sure to record your answers,
so that you can upload your completed lab sheet.